Phase transition between turbulence and zonal flows in the Hasegawa-Wakatani system.

21 May. 2025

Synthetic figure of the hysteresis observed in the phase transition between 2D turbulence ("hot'' state) and the quasi-1D state dominated by zonal flows ("cold'' state).

The Hasegawa-Wakatani system is a simplified model for instability-driven 2D turbulence in the edge of tokamak magnetised plasmas [1]. In this system, a dissipative drift-wave linear instability is generated by a background density gradient, which acts as a “free energy”' source, and then saturates into 2D turbulence which can self-organise into zonal flows, which are large-scale, 1D sheared flows.

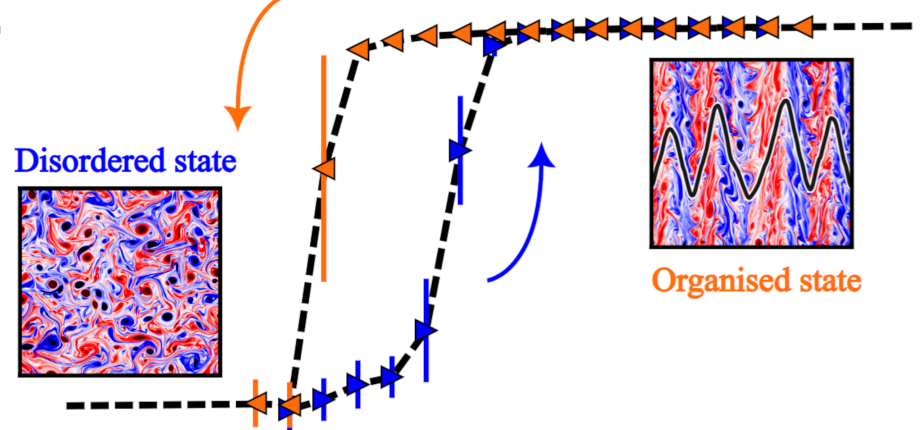
The model contains two linear parameters: i) the adiabaticity parameter, which couples the electrostatic potential and the density fluctuations, and ii) the background density gradient . The ratio constrains the regime in which the system may be. For , the system is close to 2D isotropic turbulence, which can be qualified as a disordered “hot” state, in the sense of thermodynamics. On the contrary, it is dominated by zonal flows for and becomes quasi-1D. This organised state can be seen as a “cold” crystalline structure.

Using numerical simulations and performing an extensive linear parameter scan, we study the phase transition between those two regimes, by identifying as the control parameter of the transition, and the fraction of kinetic energy contained into the zonal flows as the order parameter [2]. In simulations during which is varied, we evidence the hysteresis that the system exhibits around the transition point, illustrated in the Figure, which suggests that some latent heat is required to “destroy” the zonal structure once it has been formed, and hints to a 1^st order transition.

We then develop a reduced model, composed of 12 Fourier modes, which seems to be the minimal model able to reproduce the transition, since it includes a mechanism of energy transfer to the zonal flows, but also some interactions between turbulent modes which are able to transfer energy to the large turbulent scales, which constitutes a process similar to the 2D inverse cascade.

[1] A. Hasegawa & M. Wakatani, Phys. Rev. Lett., 50, 682 (1983)

[2] P. L. Guillon & Ö. D. Gürcan, Phys. Plasmas, 32, (1) : 012306 (2025)