Transition de phase entre écoulements zonaux et turbulence dans le système de Hasegawa-Wakatani

Le système de Hasegawa-Wakatani est un modèle simplifié de turbulence bi-dimensionnelle qui décrit l'évolution des fluctuations de potentiel électrostatique et de densité dans les plasmas magnétisés de tokamaks [1]. Dans ce système, une instabilité linéaire d'onde de dérive due à un gradient de densité génère de la turbulence 2D, qui peut s'auto-organiser en écoulements zonaux cisaillés et uni-dimensionnels.

Les deux paramètres linéaires du modèle, à savoir le paramètre d'adiabaticité  qui couple les fluctuations de potentiel électrostatique à celles de la densité, et le gradient de densité  , contraignent le régime dans lequel le système se trouve. Pour , le système est proche de la turbulence 2D isotropique, un état désordonné “chaud”. En revanche, pour , il est dominé par les écoulements zonaux et devient quasiment 1D. On peut alors l'apparenter à une structure cristalline "froide".

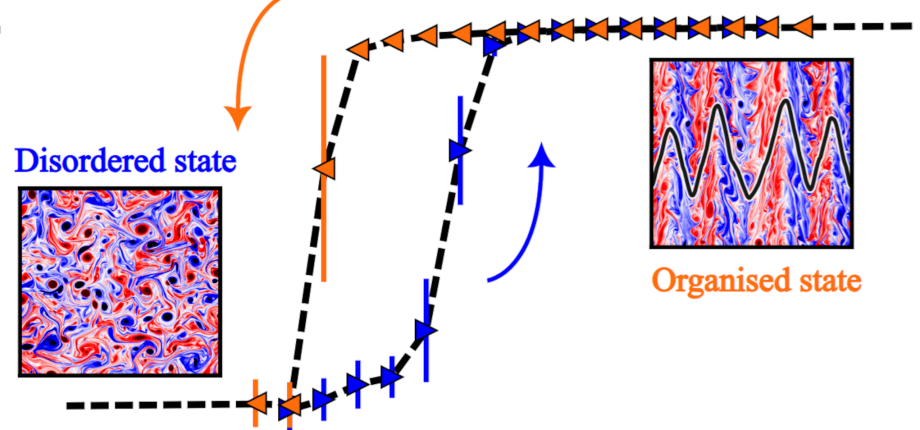
A l'aide de simulations numériques, nous étudions la transition de phase entre ces deux régimes, en identifiant  comme paramètre de contrôle de la transition, et la fraction d'énergie cinétique contenue dans les écoulements zonaux  comme paramètre d'ordre [2]. Nous mettons en évidence une hystérésis que présente le système autour du point de transition, illustrée dans la Figure, ce qui suggère l'existence d'une chaleur latente nécessaire pour "détruire" la structure zonale, une fois celle-ci formée.

Nous développons ensuite un modèle réduit, constitué de 12 modes de Fourier, qui semble être le modèle minimal capable de reproduire cette transition, car il contient des méchanismes non-linéaires de transfert d'énergie vers les écoulements zonaux, mais aussi vers les grandes échelles turbulentes.

[1] A. Hasegawa & M. Wakatani, Phys. Rev. Lett., 50, 682 (1983)
[2] P. L. Guillon & Ö. D. Gürcan, Phys. Plasmas, 32, (1) : 012306 (2025)